使用 OpenMP 做数组聚合（ Reduce ）

最近写代码遇到的一个比较实用的问题，即怎样使用 OpenMP 来做多个数组的同步聚合。我们都知道 MPI 编程中有一个函数 MPI_Allreduce 将多个分布式结点（或进程）上的数组进行聚合，然后再分发给每个结点。 MPI_Reduce 则不进行分发操作而只是把其他进程上的数组聚合到根进程上。聚合可以是数组的每个对应的元素进行相加相乘等等常用的二元操作。

但这样的操作在轻量级的 OpenMP 线程并行中如何实现呢？ OpenMP 本身提供了一些用于聚合的宏，那就是 reduction(reduction-identifier:list) ，它可用于简单的变量聚合操作。比如，我有一个超大的数组：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
#include <random>
#include <ranges>

// 生成一个带 1000 个随机数的 std::vector<int>
std::vector<int> nums;
nums.reserve(1000);
std::random_device rd{};
std::mt19937 rng{ rd() };
std::uniform_int_distribution<int> dist(0, 1000 - 1);
for (auto i : std::views::iota(0, 1000)) {
  nums.emplace_back(dist(rng));
}

现在想并行地找到其中最大的元素，用 OpenMP 可以这么写：

1
2
3
4
5
6
7
int max_value{};
#pragma omp parallel for reduction(max : max_value)
for (int i = 0; i < nums.size(); ++i) {
  if (nums[i] > max_value) {
    max_value = nums[i];
  }
}

指定聚合的操作为 max ，聚合的变量名为 max_value ，这样在每个线程内部取最大值的操作执行完毕后，程序还将把多个线程之间的最大值再比一个大小，获得全体元素的最大值。

事实上，实现这种功能或许用不到 OpenMP ，因为现在的 C++ 已经在标准库里支持这种并行查找最大值的功能了，那就是使用 std::max_element ：

1
2
3
4
5
#include <algorithm>
#include <execution>

// 使用标准库来并行查找最大值
int max = *std::max_element(std::execution::par, nums.begin(), nums.end());

通过指定执行策略为 std::execution::par ，我们把求一个数组中最大元素的执行模式变成了并行。注意， std::max_element 返回的是最大元素对应的 迭代器 ，要解引用才能获得最大元素的值。

还应注意，当前用于 Range 的取最大值操作 std::ranges::max_element 还不支持指定执行模式，这也是我没有直接用这个函数的原因。

那么我如果有一个更复杂的需求，比如将多个线程中的数组按位置聚合到一个数组里去呢？事实上这种需求并不罕见，比如每个线程都要对同一个数组做修改，由于冲突写问题无法将这个数组共享在多个线程之间，而在写的时候加锁这种方法又对并行性破坏太大，这时将每个线程本地的数组聚合起来的操作就显得重要了。因为我可以在每个线程本地创建一个数组，本地的数组不存在冲突写问题，而在线程执行完之后将本地数组聚合到全局数组上去，这个聚合操作可以是加锁的。这时就把开销最大的计算操作并行起来，而最后的串行聚合的操作开销就微不足道了。

举个例子，比如我想统计上面 nums 数组元素的分布情况，即在 0~99, 100~199, …, 900~999 这十个区间里的各有多少个元素。按上述的方法可以这样来写：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
int cnt[10]{};
#pragma omp parallel
{
  // 创建线程本地的计数数组
  int local_cnt[10]{};
#pragma omp for schedule(static)
  for (int i = 0; i < 1000; ++i) {
    ++local_cnt[nums[i] / 100];
  }
  // 在临界区中进行累加聚合
#pragma omp critical
  {
    std::ranges::transform(cnt, local_cnt, &cnt[0], std::plus<>{});
  }
}

代码中的 transormer 函数用到了它下面的重载形式：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
template< ranges::input_range R1,
          ranges::input_range R2,
          std::weakly_incrementable O,
          std::copy_constructible F,
          class Proj1 = std::identity, class Proj2 = std::identity >
requires std::indirectly_writable<O,
             std::indirect_result_t<F&,
                 std::projected<ranges::iterator_t<R1>, Proj1>,
                 std::projected<ranges::iterator_t<R2>, Proj2>>>
constexpr binary_transform_result<ranges::borrowed_iterator_t<R1>,
                                  ranges::borrowed_iterator_t<R2>, O>
    transform( R1&& r1, R2&& r2, O result, F binary_op,
               Proj1 proj1 = {}, Proj2 proj2 = {} );

摘自 cppreference 。

它接收两个 range ，对它们对应的每个元素调用 binary_op 后写到 result 所指的迭代器里。后面的两个投影函数分别是在两个 range 上进行投影。这里一个最大的坑是 result 是一个迭代器 。这意味着下面的方法是错误的：

1
2
3
4
5
std::vector<int> vec1;
std::vector<int> vec2;
// 将 vec2 累加到 vec1 上
// 下面的方法是错误的！
std::ranges::transform(vec1, vec2, vec1, std::plus<>{}); // 错误！

这是因为 vec1 并不是一个迭代器，正确的写法是：

1
2
// 将 vec2 累加到 vec1 上
std::ranges::transform(vec1, vec2, vec1.begin(), std::plus<>{}); // 正确

或者新建一个 std::vector 来存结果：

1
2
std::vector<int> vec3;
std::ranges::transform(vec1, vec2, std::back_inserter(vec3), std::plus<>{});

POD 的数组之所以可行是因为数组名作为变量时本身就是一个指针（迭代器）：

1
2
3
4
5
6
7
8
int arr1[10]{};
int arr2[10]{};
// 将 arr2 累加到 arr1 上
std::ranges::transform(arr1, arr2, arr1, std::plus<>{}); // 正确
// 显式地指名这是一个指针
std::ranges::transform(arr1, arr2, &arr1[0], std::plus<>{}); // 正确
// 直接包装成一个迭代器
std::ranges::transform(arr1, arr2, std::begin(arr1), std::plus<>{}); // 正确

为了避免犯错，还是使用下面两种写法比较好。

于是，我们能归纳出一个模板出来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
std::vector<int> data; // int 可以替换成任意类型
#pragma omp parallel
{
  // 创建线程本地的计数数组
  std::vector<int> local_data;
  // 在下面进行复杂的计算操作
  // 注意操作只能更新 local_data
  // ...

  // 在临界区中进行累加聚合
#pragma omp critical
  {
    // std::plus<>{} 可以替换成任意二元运算
    std::ranges::transform(data, local_data, data.begin(), std::plus<>{});
  }
}

这个模板可以用在很多类似的场景中。有人可能会问为什么不用 OpenMP 提供的自定义 reduction 特性，即 #pragma omp declare reduction ，我觉得两种方法都可以，但如果只做数组的聚合，那么显然上面的方法要更加简洁一些。如果是在自定义的类上做聚合，那应当去用 OpenMP 提供的这个特性。

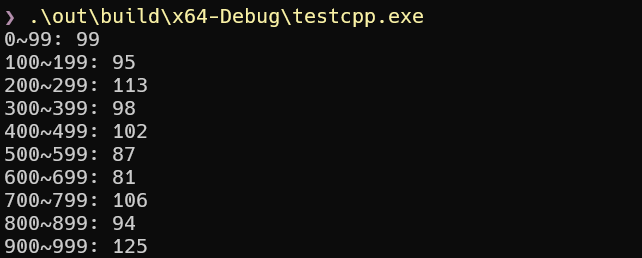
有始有终，让我们输出上面数组元素分布情况的统计结果：

1
2
3
for (auto i : std::views::iota(0, 10)) {
  std::cout << std::format("{}~{}: {}", 100 * i, 100 * (i + 1) - 1, cnt[i]) << std::endl;
}

运行结果如下：

文章目录